
#include <phrand.h>
Inheritance diagram for simth::ExponentialMaxLimitRng:

Public Member Functions | |
| ExponentialMaxLimitRng (double lambda, double Tmax) | |
| virtual | ~ExponentialMaxLimitRng () |
| virtual double | get () const |
| double | attenuationFactor () const |
| double | maxLimit () const |
With given attenuation 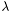 and an upper interval bound
and an upper interval bound 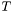 the probability density function (pdf) of this random variable will be
the probability density function (pdf) of this random variable will be
![\[ f(x) = \left\{ \begin{array}{cl} 0 & \mbox{for } x<0, x>T \\ \frac{\lambda}{1-e^{-\lambda T}} e^{-\lambda x} & \mbox{for }0\le x\le T \end{array} \right. \]](form_26.png)
The attenuation lambda and the upper interval bound T are given as constructor parameters.
For this truncated exponential, the mean value is
![\[\mu_{tr}=\frac{1}{\lambda} - T\frac{1}{e^{\lambda T}-1}\]](form_27.png)
(note the positive exponent in the denominator) and the variance is
![\[ \sigma_{tr}^2 = \frac{1}{\lambda^2} - (T^2+\frac{T}{\lambda})\frac{1}{e^{\lambda T}-1}\]](form_28.png)
The cumulative distribution function (CDF) is
![\[ F(x) = \int_{-\infty}^xf(t)dt = \left\{ \begin{array}{cl} 0 & \mbox{for }x<0 \\ \frac{1}{1-e^{-\lambda T}}(1-e^{-\lambda x}) & \mbox{for }0\le x\le T \\ 1 & \mbox{for }x>T \end{array} \right. \]](form_29.png)
This PDF of a truncated exponential will approximately come close to the usual non-truncated exponential if the upper interval bound T is greater than roughly 6.5 times the mean value, i.e. if the condition  holds. This bound is derived by calculating how much greater T must be compared to
holds. This bound is derived by calculating how much greater T must be compared to 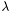 , so that the second term of the mean value
, so that the second term of the mean value 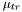 is smaller than a given fraction of the first term. The required multiple turns out to be calculated by the -1th branch of Lambert's W function of the precision, e.g. for 0.01 in Matlab
is smaller than a given fraction of the first term. The required multiple turns out to be calculated by the -1th branch of Lambert's W function of the precision, e.g. for 0.01 in Matlab -lambert(-1,-0.01)
If this condition is met, the usual formulas for the exponential distribution will hold: The probability density function (pdf) is 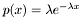 for
for 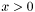 and
and  elsewhere, the mean value is
elsewhere, the mean value is  , and the variance is
, and the variance is 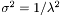 .
.
WATCH OUT: The constructor takes the attenuation as an argument, not the mean value. Even in earlier versions, when the documentation errornously said it would take the mean, it still took the attenuation. Please make really sure you understand that you have to specify the attenuation here and not the mean.
This RNG simply uses a uniform RNG from the GSL, and takes this as input to the inverse cumulative distribution function (CDF) of the truncated exponential CDF. This means if 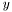 is a [0,1[-uniform random variable, the truncated exponential random variable
is a [0,1[-uniform random variable, the truncated exponential random variable 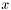 is calculated as
is calculated as
![\[ x = F^{-1}(y) = -\frac{1}{\lambda}\ln\left(1-y(1-e^{-\lambda T})\right) \]](form_39.png)
Previously it was stated here that the 'maximally equidistributed combined Tausworthe generator by L'Ecuyer' is used to generator the random output. (See GSL reference manual for further information).
|
||||||||||||
|
Class constructor with attenuation factor 'lambda' and maximal generated value 'T'.
|
|
|
Destructor |
|
|
Returns a random variate with the described exponential distribution. Implements simth::RandomGenerator. |
|
|
Attenuation factor (lambda) of the distribution (approx. = 1/mean). |
|
|
|
 1.4.1
1.4.1