|
Namespaces |
| namespace | mimo |
Complex Matrix operations |
| int | real_size (const CMatrix &, int complex_size) |
| const Complex & | c_assign (CMatrix &A, int i, int j, const Complex &c) |
| Complex | c_access (const CMatrix &A, int i, int j) |
| std::ostream & | c_print (std::ostream &s, const CMatrix &G) |
| int | c_size (const CMatrix &A, int dim) |
| CMatrix | c_eye (int i) |
| CMatrix | c_zeros (int i, int j) |
| CMatrix | c_ones (int i, int j) |
| const Complex & | c_add_s (CMatrix &A, int i, int j, const Complex &c) |
| simth::Complex | c_det (const CMatrix &A) |
Real-valued Matrix operations |
| Matrix | eye (int i) |
| Matrix | zeros (int i, int j) |
| Matrix | ones (int i, int j) |
| double | det (const Matrix &A) |
Complex Vector operations |
| const Complex & | c_assign (CVector &A, int i, const Complex &c) |
| Complex | c_access (const CVector &A, int i) |
| std::ostream & | c_print (std::ostream &s, const CVector &G) |
| int | c_size (const CVector &A) |
| const Complex & | c_add_s (CVector &a, int i, const Complex &c) |
| CVector | c_ones (int i) |
| CVector | c_zeros (int i) |
| Vector | zeros (int i) |
Blas routines |
All of these are originally defined inside the Blas++ headers. But there, they are (of course) only defined for real-valued vectors. Here we add versions that can deal with our complex vectors and matrices and also Complex numbers.
|
| void | Blas_Add_Mult (CVector &dy, const Complex &c, const CVector &dx) |
| void | Blas_Mult (CVector &dy, const Complex &c, const CVector &dx) |
| void | Blas_Scale (const Complex &c, CVector &dx) |
| Complex | Blas_Dot_Prod (const CVector &dx, const CVector &dy) |
| void | Blas_R1_Update (CMatrix &A, const CVector &dx, const CVector &dy, const Complex &alpha) |
| double | Blas_NormF (const CMatrix &A) |
| double | Blas_NormF (const Matrix &A) |
| double | Blas_Cond (const CMatrix &a, double threshold=0.0) |
| unsigned | Blas_Rank (const CMatrix &a, double threshold=0.0) |
| double | Blas_NormF_squared (const CMatrix &A) |
| void | Mat_Add_Norm (Matrix &A, const CMatrix &B) |
Defines |
| #define | LA_COMPLEX_SUPPORT |
Typedefs |
| typedef LaComplex | Complex |
| | We need a special complex type here. It has the necessary conversion operators to everything else.
|
| typedef LaGenMatDouble | Matrix |
| | Matrix of real double values.
|
| typedef LaVectorDouble | Vector |
| | Vector of real double values.
|
| typedef LaGenMatComplex | CMatrix |
| | Matrix of complex double values.
|
| typedef LaVectorComplex | CVector |
| | Vector of complex double values.
|
The matrix and vector types appear for complex and real (double) values.
Historical note: Until 2004-01-14, we used a 'pseudo-complex matrix' which in fact was a real-valued matrix of double the size. This was the reason why we invented the c_access and c_assign functions.
![\[ A_{n\times m} = \left(\begin{array}{ccc} a_{11} & & a_{1m} \\ & \ddots & \\ a_{n1} & & a_{nm} \end{array}\right) \]](form_7.png)
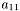 you have to write
you have to write ![\[ w_{n} = \left(\begin{array}{c} w_1 \\ \vdots \\ w_n \end{array}\right) \]](form_9.png)
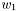 you have to write
you have to write 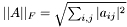 , i.e. the square root of the sum of the absolute squares of its elements.
, i.e. the square root of the sum of the absolute squares of its elements. 1.4.1
1.4.1