|
Classes |
| class | Multiply |
| | Base class for a general Multiply block. More...
|
| class | MultiplyTM |
| | Matrix Multiply implementation block. More...
|
| class | SquareTM |
| | Calculate the Product of a Matrix with itself. More...
|
| class | MultiplyInvTM |
| | Matrix inversion and multiplication block, i.e. the solution of a linear equation system. More...
|
| class | CalcCapacity |
| class | CalcSVDValues |
| class | CalcConditionNr |
| class | CalcRank |
| class | CalcMax |
| class | InvertTM |
| | Inversion of the input samples when sample are a matrix. More...
|
| class | AwgnGenerator |
| class | CalcPCSValues |
| class | ChannelEstim |
| class | EstimSingleCarrier |
| class | EstimOFDM |
| class | Equalizer |
| class | EqualizerZF |
| | ZF Equalizer, i.e. Matrix inversion and multiplication block, i.e. the solution of a linear equation system. More...
|
| class | EqualizerMMSE |
| | MMSE Equalizer, i.e. Matrix inversion and multiplication block, i.e. the solution of a linear equation system. More...
|
| class | EqualizerMRC |
| | Maximum Ratio-Combining Equalizer,. More...
|
| class | EqualizerMRCSwitch |
| | Maximum Ratio-Combining Equalizer with antenna selection on tx side. More...
|
| class | FadingMIMOChannel |
| | DEPRECATED. MIMOChannel for statistical fading model. More...
|
| class | CmplFadingMIMOChannel |
| | MIMOChannel with complex i.i.d. Gaussian fading. More...
|
| class | FileFadingChannel |
| | Fading channel which reads fading coefficients from a file. More...
|
| class | MSequenceBase |
| | Base class for implementing access to a sequence. More...
|
| class | MSequence |
| | Base class for implementing access to a sequence. More...
|
| class | MSequenceStorage |
| | Implementation of a sequence. More...
|
| class | MSequenceAccess |
| | Implementation of a shallow copy of a sequence. More...
|
| class | MSeqAttrT |
| class | MFreqSeqAttrT |
| class | MTimeSeqAttrT |
| class | VSeqAttrT |
| class | VTimeSeqAttrT |
| class | MaxEntropyChannel |
| class | MIMOChannel |
| class | PerfectMIMOChannel |
| class | AWGNMIMOChannel |
| class | AntennaArray |
| | Abstract base class that describes the geometry of the antenna array. More...
|
| class | UniformLinearLambdaHalf |
| class | UniformCircularLambdaHalf |
| class | NonUniform |
| class | Decoder |
| | Abstract base class for a MIMO symbol decoder. More...
|
| class | SpatialMuxDecZF |
| class | SpatialMuxDecMMSE |
| class | STBCAlamoutiDec |
| class | SVDDec |
| class | AntennaSelDec |
| class | RotAlamoutiDec |
| class | Encoder |
| | Abstract base class for a MIMO symbol encoder. More...
|
| class | SpatialMuxEnc |
| class | STBCAlamoutiEnc |
| class | SVDEnc |
| class | AntennaSelEnc |
| class | RotAlamoutiEnc |
| class | LsdDecoder |
| class | LsdEncoder |
| class | PCSDecoder |
| class | PCSEncoder |
| class | Multiplexer |
| | Base class for a general Multiplexer/Demultiplexer. More...
|
| class | MultiplexerT |
| | Multiplexer. More...
|
| class | MultiplexerT< CMatrixSeq > |
| class | ToVector |
| class | FromVector |
| class | MultiplexFromVector |
| class | FromDiag |
| class | FromMat |
| class | Vectorize |
| class | PathParam |
| class | WSSUSChannel |
| class | WSSUSChannelJakesUniform |
| class | WSSUSChannelExpDelay |
| class | WSSUSChannelBU |
| class | WSSUSChannelHT |
| class | WSSUSChannelScattering |
| class | WSSUSChannelFreqTimeCorr |
| class | WSSUSChannelRA |
| | WSSUS channel for a rural area (COST). More...
|
| class | WSSUSChannelTU |
| class | FileWssusChannel |
| class | WSSUSChannel2 |
| class | WSSUSChannel2JakesUniform |
| class | WSSUSChannel2ExpDelay |
| class | WSSUSChannel2Scattering |
| class | WSSUSChannel2TU |
Namespaces |
| namespace | Invert |
| namespace | MultiplexVector |
Complex Matrix operations |
| int | real_size (const CMatrix &, int complex_size) |
| const Complex & | c_assign (CMatrix &A, int i, int j, const Complex &c) |
| Complex | c_access (const CMatrix &A, int i, int j) |
| std::ostream & | c_print (std::ostream &s, const CMatrix &G) |
| int | c_size (const CMatrix &A, int dim) |
| CMatrix | c_eye (int i) |
| CMatrix | c_zeros (int i, int j) |
| CMatrix | c_ones (int i, int j) |
| const Complex & | c_add_s (CMatrix &A, int i, int j, const Complex &c) |
| simth::Complex | c_det (const CMatrix &A) |
Real-valued Matrix operations |
| Matrix | eye (int i) |
| Matrix | zeros (int i, int j) |
| Matrix | ones (int i, int j) |
| double | det (const Matrix &A) |
Complex Vector operations |
| const Complex & | c_assign (CVector &A, int i, const Complex &c) |
| Complex | c_access (const CVector &A, int i) |
| std::ostream & | c_print (std::ostream &s, const CVector &G) |
| int | c_size (const CVector &A) |
| const Complex & | c_add_s (CVector &a, int i, const Complex &c) |
| CVector | c_ones (int i) |
| CVector | c_zeros (int i) |
| Vector | zeros (int i) |
Blas routines |
All of these are originally defined inside the Blas++ headers. But there, they are (of course) only defined for real-valued vectors. Here we add versions that can deal with our complex vectors and matrices and also Complex numbers.
|
| void | Blas_Add_Mult (CVector &dy, const Complex &c, const CVector &dx) |
| void | Blas_Mult (CVector &dy, const Complex &c, const CVector &dx) |
| void | Blas_Scale (const Complex &c, CVector &dx) |
| Complex | Blas_Dot_Prod (const CVector &dx, const CVector &dy) |
| void | Blas_R1_Update (CMatrix &A, const CVector &dx, const CVector &dy, const Complex &alpha) |
| double | Blas_NormF (const CMatrix &A) |
| double | Blas_NormF (const Matrix &A) |
| double | Blas_Cond (const CMatrix &a, double threshold=0.0) |
| unsigned | Blas_Rank (const CMatrix &a, double threshold=0.0) |
| double | Blas_NormF_squared (const CMatrix &A) |
| void | Mat_Add_Norm (Matrix &A, const CMatrix &B) |
Typedefs |
| typedef LaComplex | Complex |
| | We need a special complex type here. It has the necessary conversion operators to everything else.
|
| typedef LaGenMatDouble | Matrix |
| | Matrix of real double values.
|
| typedef LaVectorDouble | Vector |
| | Vector of real double values.
|
| typedef LaGenMatComplex | CMatrix |
| | Matrix of complex double values.
|
| typedef LaVectorComplex | CVector |
| | Vector of complex double values.
|
typedef MSequence< CMatrix,
MFreqSeqAttrT< CMatrix > > | MatrixFreqSignal |
typedef MSequence< CVector,
VSeqAttrT< CVector > > | CVectorSeq |
typedef MSequence< CVector,
VTimeSeqAttrT< CVector > > | VectorTimeSignal |
typedef MSequence< CMatrix,
MTimeSeqAttrT< CMatrix > > | MatrixTimeSignal |
Functions |
| std::ostream & | operator<< (std::ostream &os, const MIMOChannel &cha) |
| std::ostream & | operator<< (std::ostream &os, const Decoder &enc) |
| std::ostream & | operator<< (std::ostream &os, const Encoder &enc) |
Variables |
class class class class class
class class typedef MSequence<
CMatrix, MSeqAttrT< CMatrix > > | CMatrixSeq |
| const double | DELAY_THRESHOLD = 0.001 |
The matrix and vector types appear for complex and real (double) values.
Historical note: Until 2004-01-14, we used a 'pseudo-complex matrix' which in fact was a real-valued matrix of double the size. This was the reason why we invented the c_access and c_assign functions.
![\[ A_{n\times m} = \left(\begin{array}{ccc} a_{11} & & a_{1m} \\ & \ddots & \\ a_{n1} & & a_{nm} \end{array}\right) \]](form_7.png)
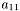 you have to write
you have to write ![\[ w_{n} = \left(\begin{array}{c} w_1 \\ \vdots \\ w_n \end{array}\right) \]](form_9.png)
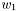 you have to write
you have to write 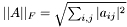 , i.e. the square root of the sum of the absolute squares of its elements.
, i.e. the square root of the sum of the absolute squares of its elements. 1.4.1
1.4.1